1656. Las chinchetas

    Profe, mire. Se me abrió la cajita de 100 chinchetas y se cayeron todas al suelo. Conté las que quedaron con la punta hacia arriba: 42... Me pregunto: si se cayeran 7, ¿cuál es la probabilidad de que quedasen 3 hacia arriba y 4 hacia abajo? 

    Pepe Chapuza tiene problemas con las chinchetas...

SOLUCIÓN

    Nina Guindilla sabía que aquí había una distribución de probabilidad binomial...

    Profe, mire. Consideremos la variable aleatoria discreta X = "número de chinchetas hacia arriba". Buscamos P(X=3). El problema es similar a tirar una sola chincheta 7 veces y que caiga 3 veces hacia arriba y 4 veces hacia abajo. Hay bastantes posibilidades de que esto ocurra... Una sería (▲▼▼▼▲▲▼) . O, si anotamos las tiradas en que sale "arriba", (1ª-5ª-6ª). Da igual cómo lo anotemos porque PR₇ ^3,4 = C_7,3 = 7!/3!/4! = 35 , es decir, hay 35 posibilidades. Solo hay que saber la probabilidad de que una chincheta quede hacia arriba. Supongamos que, por el accidente de Pepe, es 42/100 = 0,42. La probabilidad de que quede hacia abajo será 1–0,42 = 0,58. La probabilidad de cada una de esas 35 posibilidades es la misma: 0,42³·0,58⁴ (sucesos independientes). Por tanto P(X=3) = 35·0,42³·0,58⁴  = 0,2934.

    ¡Bravo! ¿Por qué se llama distribución binomial?

RESOLUCIÓN

    Yoyó Gaviota pensó en general...

    Mire, profe. En el problema anterior, X ~ Bin(7; 0,42), lo que significa que X sigue una distribución de probabilidad binomial, con 7 chinchetas y probabilidad 0,42 para "arriba". Es obvio que P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X=7) = 1. Estamos "distribuyendo" la probabilidad entre los ocho valores posibles de la variable X.

    En general, si X ~ Bin(n, p), entonces P(X=k) = C_n,k · p^k · q^n−k (donde q = 1–p). Esta fórmula es idéntica a la de un término del desarrollo del binomio de Newton de (p+q)ⁿ. Ahora está claro por qué se llama distribución binomial...

    A n se le denomina número de ensayos, p es la probabilidad del éxito y q es la probabilidad del fracaso. La esperanza y la varianza valen np y npq, respectivamente.

1655. Los círculos gemelos de Arquímedes

     Mire, profe. Dividimos en dos partes un arbelos de vértices A, B y C mediante una perpendicular a la recta ABC que pasa por B. (B está entre A y C.) Entonces, los círculos inscritos en cada parte del arbelos son iguales.

    Menos mal que Pepe Chapuza acompañó esta proposición con un dibujo. ¿Quién la quiere demostrar? 

SOLUCIÓN

    Nina Guindilla se adelantó a los demás... 

    Mire, profe. Estos se llaman los círculos gemelos de Arquímedes, y la demostración no es difícil. 

    Sean R y r los radios de las semicircunferencias AB y BC. Supongamos que R≥r. El radio de la semicircunferencia AC será R+r. Sea s el radio del círculo de Arquímedes de la derecha y consideremos los triángulos rectángulos naranja y violeta. Como tienen un cateto común, aplicando el teorema Pitágoras y la tercera identidad notable... 

(R+r−s)² − (R−r+s)² = (r+s)² − (r−s)²

2R 2(r–s) = 2r 2s

Rr = Rs+rs

s = Rr/(R+r)

    Tanto la multiplicación como la adición son operaciones conmutativas, así que, en la fórmula obtenida, R y r son intercambiables... Por tanto el radio del círculo de Arquímedes de la izquierda mide también s... y podemos decir que los círculos de Arquímedes sí son gemelos...

    Muy bien... ¿Algo más que añadir? 

RESOLUCIÓN

    Yoyó Gaviota comentó que en el arbelos se han ido descubriendo muchos círculos del mismo tamaño que los de Arquímedes con preciosas propiedades... 

    ¡Profe, si resulta que los círculos de Arquímedes no son gemelos sino multillizos...! 

1654. La danza de Selene

     Pepe Chapuza está "enamorado" de la luna (o como él dice, de Selene) en todas sus fases... Tanto, que incluso imita a los indios de las películas del oeste y dice lunas en vez de meses... Así que le pregunté cuánto duraba una luna... Y él me respondió con otra pregunta... 

    ¿Qué clase de luna: sinodal, sideral, dracónica o anómala?

    La clase se quedó estupefacta... ¡Vamos a ver cómo danza Selene!

SOLUCIÓN

    Nina Guindilla nos fue desvelando los misteriosos pasos de baile de la luna... 

    Mire, profe.

    El mes sinodal o sinódico es el tiempo que pasa entre dos adelantos de la luna al sol en la esfera celeste: 29,53 días. Sínodo significa encuentro en griego... Es también el tiempo que tarda la luna en pasar por todas sus fases. Las fases lunares se asocian al ciclo de la vida: nace, crece, mengua y muere... Este es el mes al que los indios llaman luna... 

    El mes sideral o sidéreo es el tiempo que tarda la luna en dar una vuelta completa al firmamento: 27,32 días. Se denomina firmamento porque se creía que era el firme soporte de las estrellas fijas. Sidus, sideris significa astro en latín. Si en vez de las estrellas se toma como referencia los solsticios y los equinoccios tenemos el mes trópico o tropical que es ligerísimamente menor debido a la precesión terrestre... Trópico significa vuelta en griego. 

    El mes dracónico o draconítico es el tiempo que tarda la luna en atravesar dos veces la eclíptica (la trayectoria del sol el el cielo): 27,21 días. Medio mes la luna está a un lado de la eclíptica y el otro medio mes está al otro lado. Los puntos de cruce se llaman nodos y los eclipses se producen en ellos, de ahí el nombre de eclíptica. Según un antiquísimo mito, es un dragón el que se come al sol o a la luna y por eso se dice mes dracónico...

    El mes anómalo o anomalístico es el tiempo que tarda la Luna en atravesar dos veces la línea de ápsides de su órbita elíptica: 27,55 días. Los ápsides son el perigeo y el apogeo que son los puntos donde la luna más se acerca y más se aleja, respectivamente, de la tierra, ya que esta se halla en uno de los focos de la elipse. El mes se denomina anómalo en el sentido de extraño...

    Pero lo más enigmático es que la luna tarda lo mismo en realizar una rotación que una traslación, por eso siempre da la cara y nunca nos da la espalda... 

    Después de la intervención de Nina pregunté cómo se aprendió cada uno el número de días que tienen los meses de nuestro calendario... 

RESOLUCIÓN

    La mayoría de los alumnos contestó que fue con los nudillos de las manos o con alguna retahíla. Pero Yoyó Gaviota lo hizo con las teclas del piano... 

    Profe, mire. Si empezamos en la nota fa, las teclas blancas corresponden a meses de 31 días y las negras a los de menos días... 

    Se deja al lector interesado que investigue los movimientos de la tierra, esto es, la danza de Gea... (traslación, rotación, precesión, nutación y alguno más).

1653. Girando los símbolos

     Mire, profe. En el suceso condicionado A|B estamos suponiendo B. En el suceso diferencia A\B estamos excluyendo B. Encuentro cierta relación entre las dos operaciones... De hecho las fórmulas de sus probabilidades se parecen:

P(A|B) = P(A⋂B) / P(B) 

P(A\B) = P(A⋃B) − P(B)

    Es como si girásemos los símbolos de las operaciones...

    No hace falta que os diga que Pepe Chapuza no dejará de sorprenderme... ¿Girar los símbolos?

SOLUCIÓN

    Nina Guindilla le siguió la corriente a Pepe...

    Profe, mire lo que sucede con varios sucesos... Si cambiamos ahora la multiplicación por la suma... girando... 

P(A⋂B⋂C...) = P(A) × P(B|A) × P(C|(A⋂B))...

P(A⋃B⋃C...) = P(A) + P(B\A) + P(C\(A⋃B))...

    ¿Alguna fórmula más? 

RESOLUCIÓN

    Profe, mire lo que pasa girando los símbolos... 

    Si P(A|B) = P(A) entonces A y B son independientes, y P(A⋂B) = P(A) × P(B).

    Si P(A\B) = P(A) entonces A y B son incompatibles, y P(A⋃B) = P(A) + P(B).

    Yoyó Gaviota terminó por convencerme... Al menos sirve para aprenderse las fórmulas... 

1652. Los poliedros de Kepler-Poinsot

     Profe, mire. Hay una sola clase de triángulos regulares (los equiláteros) y una sola clase de cuadriláteros regulares (los cuadrados), pero de pentágonos regulares tenemos dos clases (los convexos y los estrellados). Podemos seguir analizando los polígonos regulares... Hay infinitos... convexos y estrellados... A lo que voy...

    Aunque hay infinitos polígonos regulares, solo hay cinco poliedros regulares (los platónicos) y en ellos solo intervienen los triángulos equiláteros, los cuadrados y los pentágonos regulares convexos. ¡Los demás polígonos están vedados! 

    Interrumpí a Pepe Chapuza para que no siguiera divagando... Le comuniqué que los cinco sólidos platónicos eran poliedros regulares convexos... pero que existían los cuatro poliedros de Kepler-Poinsot, que también eran regulares pero que no eran convexos y... ¡en dos de ellos participaba el pentágono regular estrellado!, y que por lo tanto este polígono no estaba vedado...

    Buscad los poliedros de Kepler-Poinsot.

SOLUCIÓN

    Nina Guindilla trajo al día siguiente una presentación de los poliedros de Kepler-Poinsot:

    Profe, mire. Al igual que los lados de un polígono estrellado están atravesados por otros, eso mismo decimos de las caras y de las aristas de los poliedros de Kepler-Poinsot. 

    El gran icosaedro (GI) está formado por triángulos, el gran dodecaedro (GD) por pentágonos convexos y el gran dodecaedro estrellado (GDE) y el pequeño dodecaedro estrellado (PDE) por pentágonos estrellados... pero resulta difícil ver sus caras porque, como dije, están atravesadas... El GI y el GDE son duales. El GD y el PDE también...

    Nina nos mostró de cada poliedro de Kepler-Poinsot una cara atravesada por otras. Esto nos daba una idea de sus aspectos. (Hay bonitas imágenes de los cuatro en la red...)

    Ya habíamos visto que en el hiperespacio tetradimensional había seis polícoros regulares convexos, ¿cuántos polícoros regulares no convexos hay? 

RESOLUCIÓN

    Yoyó Gaviota buscó en Internet y encontró diez... 

    Resumiendo, profe. En tres dimensiones hay nueve poliedros regulares y en cuatro dimensiones hay dieciséis polícoros regulares... 

1651. El plano de Fano

    Habíamos hablado de las geometrías afines planas finitas... que se construían a partir de dos axiomas: por dos puntos separados pasa una sola recta y por un punto separado de una recta pasa una sola paralela. Y puse como ejemplo el "esqueleto" del tetraedro: cuatro puntos (los vértices) y seis rectas (las aristas). Pepe Chapuza aclaró.

    ¡Claro, profe! Las rectas paralelas son las aristas opuestas... entendiendo por paralelas que tienen intersección vacía...

    Pepe preguntó a continuación... 

    Si el segundo axioma fuera que dos rectas distintas siempre tienen un único punto común, ¿podríamos hablar de geometría proyectiva plana finita?

    La respuesta fue que sí y que un bonito ejemplo era el llamado plano de Fano... Así que ya había tema para investigar... 

SOLUCIÓN

    Nina Guindilla investigó los dos planos finitos comentados: el afín y el proyectivo...

    Mire, profe... 

    En el primer plano podemos asignar las coordenadas (0,0), (0,1), (1,0) y (1,1) a los cuatro puntos y las ecuaciones (0,T), (T,0), (1,T), (T,1), (T,T) y (T,1−T) a las seis rectas (T∈{0,1}). 

    En el segundo plano, el de Fano, hay siete puntos y siete rectas. (La circunferencia representa una recta...)

    Como cabía esperar, asignamos a los puntos coordenadas homogéneas: (0,0,1), (0,1,0), (1,0,0), (0,1,1), (1,0,1), (1,1,0) y (1,1,1). Y a las rectas, las ecuaciones homogéneas x≡0, y≡0, z≡0, x+y≡0, x+z≡0, y+z≡0 y x+y+z≡0. (Módulo 2.) 

    Comenté que el plano de Fano estaba relacionado con los octoniones... Ya hay otro tema de investigación... 

RESOLUCIÓN

    Yoyó Gaviota es buen investigador... 

    Mire, profe... En lo que sigue las letras minúsculas cursivas representan unidades imaginarias, las redondas minúsculas son números reales, las redondas mayúsculas son complejos y las cursivas mayúsculas son cuaterniones... 

    Pues bien. Los números complejos son binomios a+bi.

    Del mismo modo, los cuaterniones son binomios P+Qj.

P+Qj = a+bi+(c+di)j = a+bi+cj+dk

...porque ij = k. Sabemos que los productos de las unidades imaginarias se representan así:

    Pues bien, los octoniones son binomios U+Vl.

U+Vl = P+Qj+(R+Sj)l = a+bi+cj+dk+(e+fi+gj+hk)l = a+bi+cj+dk+el+fm+gn+ho

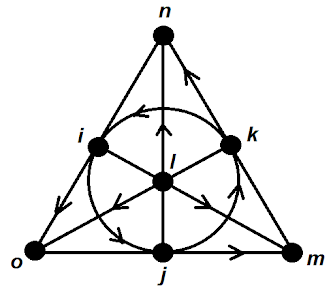
...y ya van siete unidades imaginarias... Sus productos se pueden representar con este diagrama:

    ¿Lo ve? ¡Es el plano de Fano!

    Yoyó comentó que el proceso de crear más binomios añadiendo unidades imaginarias puede continuar con los sedeniones, los trigintaduoniones... 

1650. Infinitésimos...

     Profe, mire. La primera pareja de la tabla de infinitésimos equivalentes en x = 0 es  

senx ~ x 

lo cual significa que ambos se anulan pero que lim_x→0 ( senx / x ) = 1. Esto es obvio porque la indeterminación 0/0 se puede resolver con la regla de L'Hôpital: cos0 / 1 = 1. Pero los infinitésimos se ven antes que las derivadas por lo que habría que justificar este límite sin derivar... 

    Ya conocemos a Pepe Chapuza... ¿Quién lo justifica sin derivar?

SOLUCIÓN

    Nina Guindilla dibujó el primer cuadrante del círculo unidad y dos triángulos... 

    Mire, profe. El triángulo OAC es menor que el sector circular OAC que a su vez es menor que el triángulo OBC. Si x es el ángulo común en O, entonces las tres áreas ordenadas son...

senx / 2 < x / 2 < tgx / 2

...multiplicando por 2 / senx... 

1 < x / senx < 1 / cosx

...e invirtiendo... 

1 > senx / x > cosx

    Y cuando x tiende a 0 (sería en principio por la derecha porque estamos en el primer cuadrante..., pero por la izquierda, en el cuarto cuadrante, es similar)...

1 ≥ lim_x→0 ( senx / x ) ≥ 1

Con lo que queda justificado el límite... Se podría decir que senx / x tiene una discontinuidad evitable en x = 0. De hecho es una función curiosa: se anula en todos los números enteros multiplicados por π... excepto en el 0.

    Y Nina hizo un esbozo chapucero de la gráfica... pero me bastaba para lo que pretendía... Comenté que la discontinuidad evitable se podía evitar definiendo la función f:

 f(x) = senx / x    si x ≠ 0

 f(0) = 1

    Y pedí integrar f... sin especificar el tipo de integral... Esta es una de esas funciones enrevesadas del Análisis... 

RESOLUCIÓN

    Yoyó Gaviota no cayó en la trampa... 

    Mire, profe. Se sabe que no se puede escribir una primitiva de f en función de funciones elementales. Pero sí se puede calcular la integral definida impropia

I =ഽ_−∞^∞  f(x) dx

    ¿De algún modo sería la diferencia entre las áreas azules y las rosas...? De hecho la integral se puede hacer de varias maneras... La forma siguiente me gusta, mire... Como f es una función par...

I = 2ഽ₀^∞  senx / x dx

Inserto el factor − e^−x·∞  + e^−x·0 (es 1 porque entre los límites de integración x>0)

I = 2ഽ₀^∞ senx (−e^−x·∞ + e^−x·0) / x dx

Aplico la regla de Barrow (al revés) y el teorema de Fubini (alegremente)

I = 2ഽ₀^∞  senx ഽ₀^∞ e^−xy dy dx = 2ഽ₀^∞ഽ₀^∞ e^−xy senx dx dy

Hago la integral indefinida J = ഽ e^−xy senx dx  por partes (d e^−xy = −e^−xy y dx, d senx = cosx dx, d cosx = −senx dx)

J = − e^−xy cosx − e^−xy y senx − y² J = −e^−xy ( cosx + y senx ) / ( 1 + y² )

Como la y también es positiva y el seno y el coseno son funciones acotadas...

J|₀^∞ = (−e^−∞·y (¿cos∞? +  y ¿sen∞?) + e^−0·y (cos0 +  y sen0)) / (1 + y²) = 1 / (1 + y²)

Y por tanto

I = 2ഽ₀^∞ 1 / ( 1 + y² ) dy = 2arctg∞ − 2arctg0 = 2π/2 = π

    Precioso resultado... a pesar de las cosas raras de Yoyó... Esta es la llamada integral de Dirichlet. El lector riguroso puede añadir el rigor que precise... 

1649. La diferencia simétrica

     Mire, profe. Si llamamos madrileños a los que viven en la capital y madridistas a los seguidores del equipo merengue..., y si juntamos a los madrileños que no son madridistas con los madridistas que no son madrileños... tenemos la diferencia simétrica de madrileños y madridistas:

A △ B  =  (AヽB) ∪ (BヽA)

    Pepe Chapuza había puesto un curioso ejemplo de esta operación entre conjuntos... ¿Qué propiedades tiene la diferencia simétrica?

SOLUCIÓN

    Nina Guindilla expuso que estábamos ante un grupo abeliano... 

    Profe, mire. 

    La diferencia simétrica es conmutativa. Basta con ver el diagrama de Venn simétrico que dibujó Pepe: A△B = B△A . 

    También es asociativa. Basta con ver el diagrama de Venn que he dibujado yo: A△B△C sin necesidad de paréntesis. Si C son los nacidos en Madrid (matritenses) entonces un madrileño madridista matritense está en A△B△C...

    El elemento neutro de la diferencia simétrica es el conjunto vacío, obviamente: A△Ø = A .

    El elemento simétrico de cada conjunto es él mismo: A△A = Ø . La diferencia simétrica es nilpotente. 

    Hay otra forma de definir la diferencia simétrica... 

RESOLUCIÓN

    Profe, mire. Una forma equivalente para la diferencia simétrica es

A △ B  =  (A ∪ B)ヽ(A ⋂ B) 

    Esto está relacionado con el operador booleano XOR. Así, los elementos de A△B o bien son madrileños o bien son madridistas pero no ambas cosas a la vez... 

    Profe, mire. Un elemento pertenece a la diferencia simétrica de varios conjuntos si y solo si pertenece a una cantidad impar de ellos... 

    Yoyó Gaviota nos mostró lo "caprichosa" que es la diferencia simétrica...