1573. Los teselados semirregulares

     Nos recordó Pepe Chapuzas que sólo había tres tipos de teselados regulares. 

    Mire, profe. Los teselados regulares tienen que cumplir las siguientes condiciones:

    - Han de estar formados por polígonos regulares iguales.

    - Han de ser capaces de rellenar el plano sin solapes ni huecos.

    - Los polígonos han de acoplarse juntando aristas con aristas y vértices con vértices. 

    

    Para ilustrar la tercera condición puso ejemplos...

    Y de paso ya teníamos dos de los tres tipos de teselados regulares: el formado por triángulos equiláteros y el formado por cuadrados. El tercero está formado por hexágonos regulares...

    Mire, profe. No puede haber más teselados regulares. Si los polígonos tienen más de seis lados entonces en cada vértice se juntan al menos tres ángulos mayores de 120º y se solaparían. Con cuatro pentágonos también se solaparían: 4·108º = 432º > 360º. Y con tres pentágonos quedarían huecos: 3·108º = 324º = 360º − 36º. 

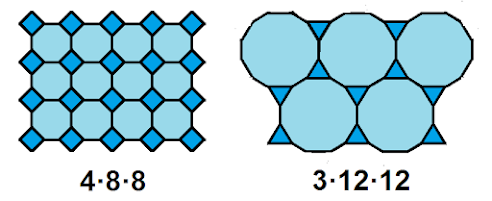
    Mire, profe. ¿Y si permitimos teselados con varios tipos de polígonos regulares con tal de que su ensamble en cada vértice siga siempre la misma disposición? 

    Esos eran los teselados semirregulares... ¿De cuántos tipos hay?

SOLUCIÓN

    Nina Guindilla encontró ocho. 

    Mire, profe. Los diferentes tipos de teselados semirregulares quedan determinados por la disposición de los poliedros alrededor de un vértice. Los teselados regulares serían 3·3·3·3·3·3, 4·4·4·4 y 6·6·6.

    Y los semirregulares:

    ¿Seguro que no hay más?

RESOLUCIÓN

    Yoyó Gaviota tenía la última palabra...

    Profe. mire. El teselado 3·3·3·3·6 es quiral, por lo que hay dos versiones. En este sentido habría 9 tipos de teselados semirregulares...