Pepe Chapuza sabía que el tema de integrales daba miedo, así que se propuso asustar:
Profe, mire que integral...
SOLUCIÓN
Nina Guindilla no tardó en coger al toro por los cuernos...
ex = x0/0! + x1/1! + x2/2! + x3/3! +
x4/4! + x5/5! + ···
e = 1 + 1 + 1/2 + 1/3! + 1/4! + 1/5! + ···
¡Bravo!
No se fue Nina sin plantear otra belleza integral...
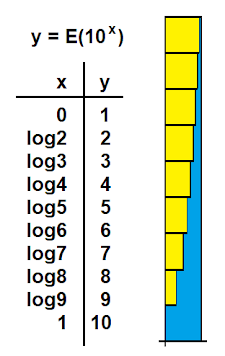
Profe, mire. Si E es la función "parte entera" calcule ʃ01 E(10x) dx .
Profe, mire. Se trata de la integral definida de una función escalonada. En el dibujo se comprueba que el área que buscamos (la azul) es (el rectángulo menos la amarilla):
9 − log2 − log3 − log4 − log5 − log6 − log7 − log8 − log9 =
= 9 − (log2+log3+log4+log5+log6+log7+log8+log9) =
= 9 − log(2·3·4·5·6·7·8·9) =
= 9 − log 9!
cuyo valor aproximado es 3,44.
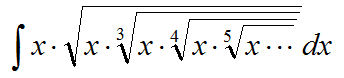
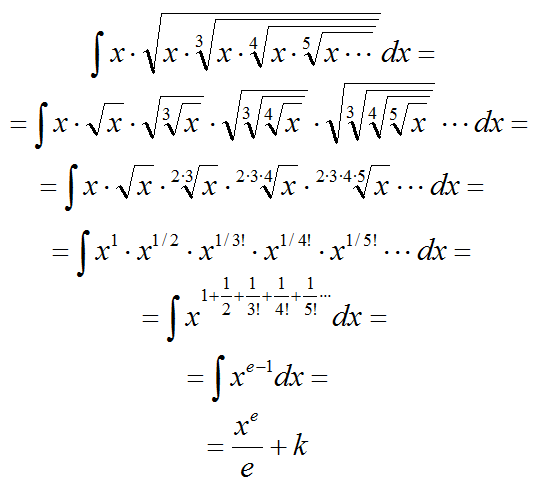
No hay comentarios:
Publicar un comentario