Pepe Chapuza nos mostró el siguiente círculo mágico:
Profe, mire. Aparecen los números del 1 al 32 y en cada circunferencia y en cada diámetro los números suman siempre 132 (66 en cada semicircunferencia y en cada radio)...
Mire, profe. Se puede poner esta misma disposición en una esfera (sería una esfera mágica), distribuyendo los números en paralelos y meridianos...
En realidad, eran modificaciones de cuadrados mágicos. ¿Puedes traer a clase alguna figura mágica?
SOLUCIÓN
Nina Guindilla trajo una estrella mágica de siete puntas y dos vueltas:
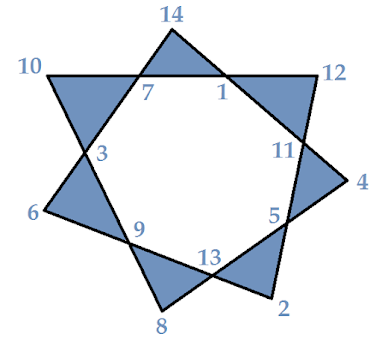
Mire, profe. Se sabe que no hay estrellas mágicas de cinco puntas (con los números del 1 al 10). Y la estrella mágica de seis puntas es archiconocida... Así que he aquí mi estrella mágica favorita...
¿Alguna aportación más?
RESOLUCIÓN
Yoyó Gaviota se presentó con dos estrellas mágicas más: la de ocho puntas y la de nueve, ambas de dos vueltas...
Mire, profe. En una estrella mágica de N puntas aparecen los números del 1 al 2N. La suma de todos estos números es N·(2N+1), así que la suma en cada lado es 2·(2N+1) = 4N+2. Esto se puede comprobar con las estrellas de 7, 8 y 9 puntas que hemos visto:
4·7 + 2 = 30
4·8 + 2 = 34
4·9 + 2 = 38
Sigue buscando la magia de las matemáticas...
No hay comentarios:
Publicar un comentario