Hay resultados matemáticos realmente sorprendentes. Pepe Chapuza expuso en la clase el teorema de Holditch...
Mire, profe... Así lo enunció el propio Holditch:
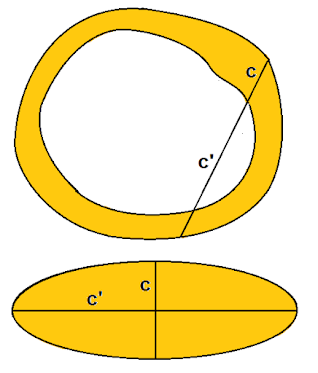
"Si una cuerda de una curva cerrada, de longitud constante c+c', se divide en dos partes de longitudes c, c' respectivamente, la diferencia entre las áreas de la curva cerrada, y el lugar geométrico del punto de división, será πcc'."
Hay que perdonar que el enunciado omita las hipótesis, que se presuponen en la demostración, acerca de las curvas y de la cuerda... El teorema es increíblemente hermoso, porque el área que nos da es la de una elipse de semiejes c y c' aunque la curva inicial no esté emparentada con las elipses...
La demostración de Holditch no era menos hermosa... Primero tenemos que recordar cómo se puede calcular el área que barre un segmento tangente, a una curva cerrada convexa orientada, de argumento θ ∈ [0, 2π] y módulo t(θ), función suave, tal que t(0) = t(2π); es decir, el área de la corona entre la curva cerrada convexa y la curva en que se apoyan los extremos de los segmentos tangentes, que es una curva cerrada simple.
SOLUCIÓN
Nina Guindilla nos lo recordó:
Mire, profe. Podemos dividir la corona mediante segmentos tangentes a la curva interior en regiones parecidas a triángulos. Si tenemos dos segmentos tangentes próximos con argumentos θ y θ' y módulos t(θ) y t(θ'), el área de la región parecida a un triángulo será aproximadamente 1/2·t(θ)·t(θ')·sen(θ'−θ). Cuando θ'→θ, entonces t(θ')→t(θ), y podemos escribir el área entre las dos curvas como
ʃ 02π 1/2·t(θ)· t(θ)·sen(dθ) = 1/2 ʃ 02π t2(θ) dθ
Ya solo quedaba demostrar el teorema del reverendo Holditch...
RESOLUCIÓN
Yoyó Gaviota empezó con las hipótesis que faltaban...
Profe, mire. Vamos a exigir que la curva inicial A sea convexa y la cuerda lo bastante corta para evitarle movimientos retrógrados y permitirle una revolución completa, asegurando un lugar geométrico B, del punto de división, suave y simple.
Y siguió con la demostración propiamente dicha...
Mire, profe. Consideremos, además, la envolvente orientada C de las cuerdas que será una curva convexa. C será interior a B y B interior a A. Llamemos [A], [B] y [C] a las áreas encerradas por A, B y C respectivamente. El área del teorema es [A]−[B].
Las cuerdas son tangentes a su envolvente. Por tanto, por un lado
[A]−[C] = 1/2 ʃ 02π t2(θ) dθ
pero también, por el otro lado
[A]−[C] = 1/2 ʃ 02π ( c+c'−t(θ) )2 dθ =
= 1/2 ʃ 02π ( (c+c')2+t2(θ)−2(c+c')t(θ) ) dθ =
= (c+c')2 π + 1/2 ʃ 02π t2(θ) dθ − (c+c') ʃ 02π t(θ) dθ
de donde
ʃ 02π t(θ) dθ = (c+c') π
Del mismo modo
[B]−[C] = 1/2 ʃ 02π ( t(θ)−c )2 dθ =
= 1/2 ʃ 02π ( t2(θ)+c2−2c t(θ) ) dθ =
= 1/2 ʃ 02π t2(θ) dθ + c2 π −c (c+c') π =
= 1/2 ʃ 02π t2(θ) dθ − cc' π =
= [A]−[C] − cc' π
de donde
[A]−[B] = cc' π
No hay comentarios:
Publicar un comentario