Dear Teacher:
What's the distance between the parabolae if their equations are
f(x) = x2/3 + 47/3
g(x) = − x2/6 + 10x/3
Susi Fogata did the calculations...
Dear Teacher:
These parabolae don't cut each other because the equation
x2/3 + 47/3 = − x2/6 + 10x/3
202 − 4·3·94 = − 728 < 0
f ' (s) = g ' (t)
2s/3 = − t/3 + 10/3
t = 10 − 2s
(s − t, f(s) − g(t)) · (1, f ' (s)) = 0
(s − t, s2/3 + 47/3 + t2/6 − 10t/3) · (1, 2s/3) = 0
(s − (10−2s), s2/3 + 47/3 + (10−2s)2/6 − 10(10−2s)/3) · (1, 2s/3) = 0
(3s − 10, s2/3 + 47/3 + 50/3 − 20s/3 + 2s2/3 − 100/3 + 20s/3) · (1, 2s/3) = 0
(3s − 10, s2 − 1) · (1, 2s/3) = 0
3s − 10 + 2s3/3 − 2s/3 = 0
2s3 + 7s − 30 = 0
or better
3x2 − 20x + 94 = 0
hasn't any solutions because its discriminant
If S (s, s2/3 + 47/3) is a point of the parabola f and T (t, − t2/6 + 10t/3) is a point of the parabola g , and are the nearest ones, then the slopes of f and g at S and T are equal...
2s/3 = − t/3 + 10/3
t = 10 − 2s
On the other hand, the vector TS is perpendicular to f at S ...
(s − t, s2/3 + 47/3 + t2/6 − 10t/3) · (1, 2s/3) = 0
(s − (10−2s), s2/3 + 47/3 + (10−2s)2/6 − 10(10−2s)/3) · (1, 2s/3) = 0
(3s − 10, s2/3 + 47/3 + 50/3 − 20s/3 + 2s2/3 − 100/3 + 20s/3) · (1, 2s/3) = 0
(3s − 10, s2 − 1) · (1, 2s/3) = 0
3s − 10 + 2s3/3 − 2s/3 = 0
2s3 + 7s − 30 = 0
s = 2 is the only solution because 42 − 4·2·15 = − 104 < 0 .
So, we have the points S (2, 17) and T (6, 14) and the vector TS = (−4, 3) , hence the distance is |TS| = √(16+9) = √25 = 5 .

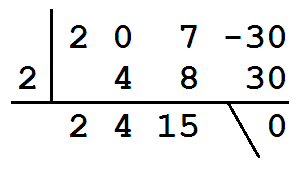
No hay comentarios:
Publicar un comentario