domingo, 31 de octubre de 2021
1575. Infinitos, quebrados y mantisas.
jueves, 28 de octubre de 2021
1574. Las matemáticas de las telarañas
Propuse para el día siguiente un trabajo en común sobre las matemáticas de las telarañas... Y al día siguiente Pepe Chapuza empezó aportando ideas:
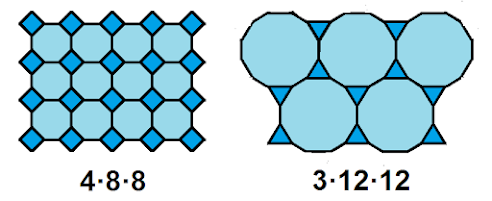
1573. Los teselados semirregulares

Mire, profe. No puede haber más teselados regulares. Si los polígonos tienen más de seis lados entonces en cada vértice se juntan al menos tres ángulos mayores de 120º y se solaparían. Con cuatro pentágonos también se solaparían: 4·108º = 432º > 360º. Y con tres pentágonos quedarían huecos: 3·108º = 324º = 360º − 36º.
miércoles, 27 de octubre de 2021
1572. El sexto polícoro
lunes, 25 de octubre de 2021
1571. De todo corazón...
1. Como la trayectoria de un punto de una circunferencia que rueda alrededor de otra circunferencia fija del mismo tamaño. (Epicicloide.)
2. Como la envolvente de los rayos reflejados, en el interior de una circunferencia fija, de los rayos emitidos desde un punto fijo de dicha circunferencia fija. (Catacáustica.)
3. Como la envolvente de las circunferencias, con centro en una circunferencia fija, que pasan por un punto fijo de dicha circunferencia fija.
Y de muchas otras formas.
Obtén la ecuación de la cardioide.
SOLUCIÓN
Nina Guindilla trabajó con coordenadas polares.
1570. Porcentajes consecutivos...
Propuse en clase un problemita y me encontré con un problemazo:
El año pasado me subieron el sueldo en un 20% y este año me lo han subido en otro 20%. ¿Qué porcentaje me subieron en los dos años?
Estaba claro que era un problema de la vida real pero no demasiado real... El caso es que la respuesta inmediata de mis alumnos fue el 40%. Menos mal que Pepe Chapuza dio un resultado distinto...
jueves, 21 de octubre de 2021
1569. El teorema del reverendo Holditch
Hay resultados matemáticos realmente sorprendentes. Pepe Chapuza expuso en la clase el teorema de Holditch...
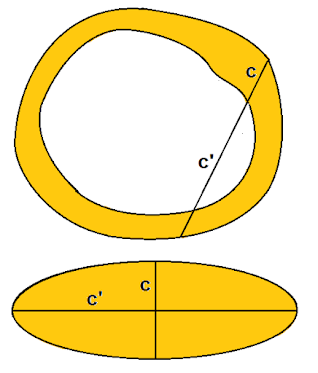
Mire, profe... Así lo enunció el propio Holditch:
La demostración de Holditch no era menos hermosa... Primero tenemos que recordar cómo se puede calcular el área que barre un segmento tangente, a una curva cerrada convexa orientada, de argumento θ ∈ [0, 2π] y módulo t(θ), función suave, tal que t(0) = t(2π); es decir, el área de la corona entre la curva cerrada convexa y la curva en que se apoyan los extremos de los segmentos tangentes, que es una curva cerrada simple.
SOLUCIÓN
viernes, 15 de octubre de 2021
1568. ¡Nuevo, nueva y... nueve!
¡Nuevo, nueva y... nueve!
¡No! Pepe Chapuza no estaba imitando a ningún político ni quería polemizar sobre el género gramatical. Había confeccionado una lista en varios idiomas:
Sigue investigando...
Yoyó Gaviota cambió de tema:
NORTE ==> 7 SUR ==> 1/2