1506. Aquiralidad. RESOLUCIÓN

    Tocaba hablar de los objetos quirales. Comenté que un objeto era quiral si no era superponible con su imagen especular... Pepe Chapuzas aclaró el concepto...

    O sea, profe. Mi mano derecha es quiral porque su imagen en el espejo, esto es, la mano simétrica respecto de un plano, es una mano izquierda y, que yo sepa, las manos derecha e izquierda no son superponibles aunque sean congruentes...

    ¡Un montón de conceptos! De hecho, la palabra "quiral" procede de la palabra griega para "mano" (como el prefijo "quiro-" de "quiromasaje" y "quiromante").
    Una vez asimilados los términos fue fácil entender lo que era un objeto aquiral: el que sí era superponible con su imagen especular... Investiga la relación entre aquilaridad y simetría...

SOLUCIÓN

    Oigamos a Nina Guindilla:

    Mire, profe... 
    En una dimensión (en la recta real) un objeto es aquiral si y solo si es simétrico respecto de un punto (el centro de la simetría central). Un objeto quiral sería por ejemplo un intervalo semiabierto (o semicerrado).

    En dos dimensiones (en el plano real) un objeto acotado es aquiral si y solo si es simétrico respecto de una recta (el eje de la simetría axial) pero hay objetos no acotados que son aquirales y asiméticos:

    En nuestro alfabeto hay unas letras mayúsculas quirales y otras aquirales... Lo mismo ocurre con las distintas piezas del tetris...

    Falta por investigar qué ocurre en tres dimensiones...

RESOLUCIÓN

    En el espacio tridimensional el asunto se complicaba como adivinó Yoyó Peluso...

    Mire, profe. 
    Una mano es un buen ejemplo de objeto quiral... (O un pie...)
    Todos los objetos que poseen simetría especular (respecto de un plano) son aquirales.

    También son aquirales todos los objetos que poseen simetría central (respecto de un punto)...

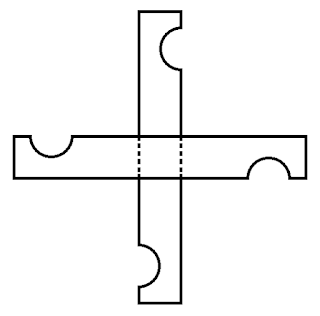
    Además hay objetos acotados aquirales que no poseen ni simetría central ni simetría especular... como el aspa siguiente construida con dos tablillas iguales...